Subgradient Methods in 10 Minutes
Now that we’ve covered topics from convex optimization in a very shallow manner, it’s time to go deeper.
Subgradient methods
What is a subgradient? It’s a substitute for the gradient, when the gradient doesn’t exist.
Convexity Review
To understand subgradients, first we need to review convexity. The Taylor series of a real valued function that is infinitely differentiable at a real number \(x\) is given by
\[f(y) \approx \sum\limits_{k=0}^{\infty} \frac{f^{(k)}(x)}{k!}(y-x)^k\]Expanding terms, the series resembles
\[f(y) \approx f(x) + \frac{f^{\prime}(x)}{1!}(y-x) + \frac{f^{\prime\prime}(x)}{2!}(y-x)^2 + \frac{f^{\prime\prime\prime}(x)}{3!}(y-x)^3 + \cdots.\]If a function is convex, its first order Taylor expansion (a tangent line) will always be a global underestimator:
\[f(y) \geq f(x) + \frac{f^{\prime}(x)}{1!}(y-x)\]If \(y=x + \delta\), then:
\[\begin{aligned} f(x+ \delta) \geq f(x) + \nabla f(x)^T (x+\delta-x) \\ f(x+ \delta) \geq f(x) + \nabla f(x)^T \delta \end{aligned}\]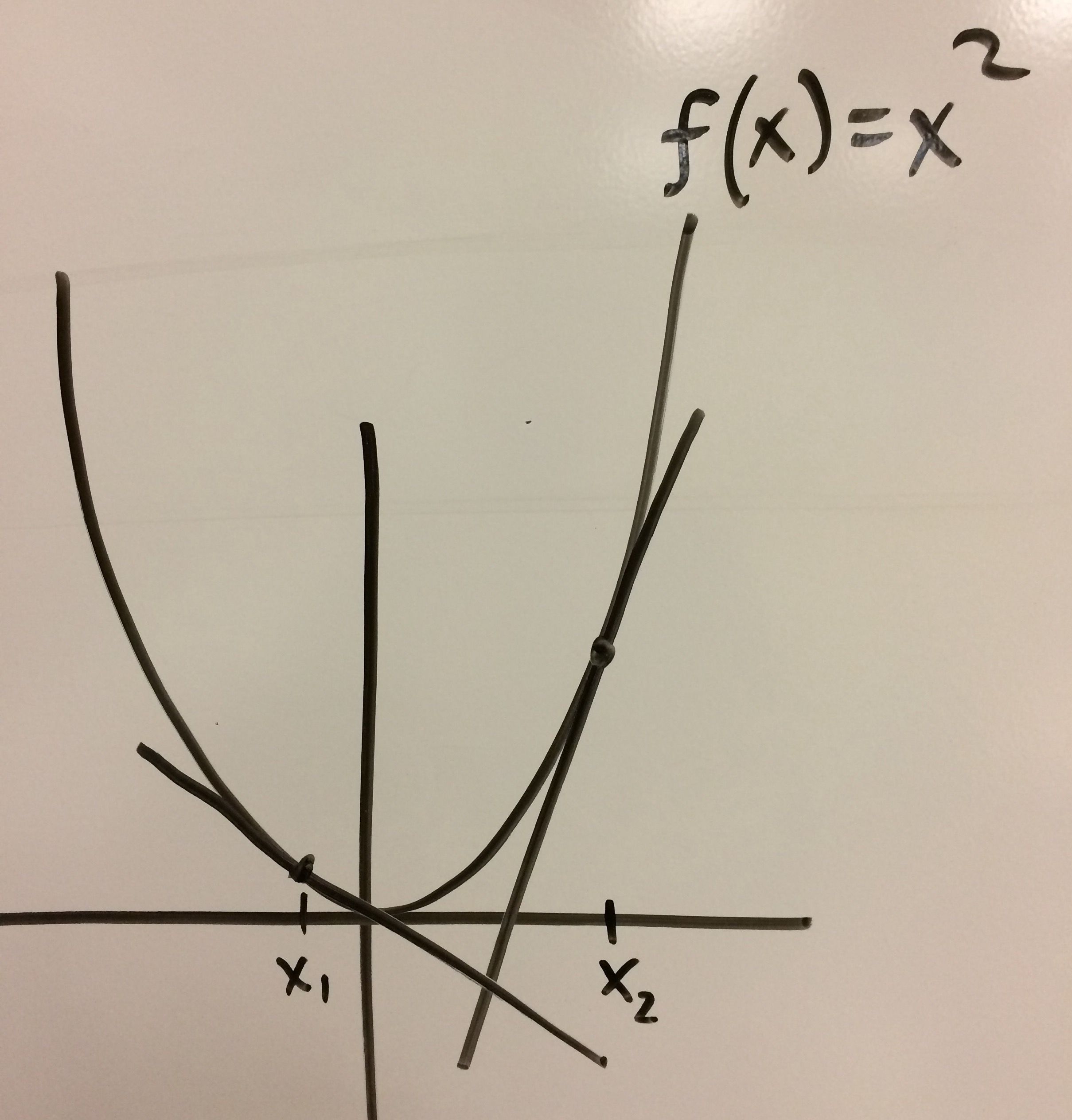
From the picture, it’s obvious that an affine function is always an underestimator for this quadratic (thus convex) function.
Subgradients
Consider a function \(f\) with a kink inside of it, rendering the function non-differentiable at a point \(x_2\).

The derivative jumps up by some amount (over some interval) at this kink. Any slope within that interval is a valid subgradient. A subgradient is also a supporting hyperplane to the epigraph of the function. The set of subgradients of \(f\) at \(x\) is called the subdifferential \(\partial f(x)\) (a point-to-set mapping). To determine if a function is subdifferentiable at \(x_0\), we must ask, “is there a global affine lower bound on this function that is tight at this point?”.
- If a function is convex, it has at least one point in the relative interior of the domain.
- If a function is differentiable at \(x\), then \(\partial f(x) = {\nabla f(x)} \) (a singleton set).
For example, for absolute value, we could say the interval \( [\nabla f_{\text{left}}(x_0), \nabla f_{\text{right}}(x_0)] \) is the range of possible slopes (subgradients):
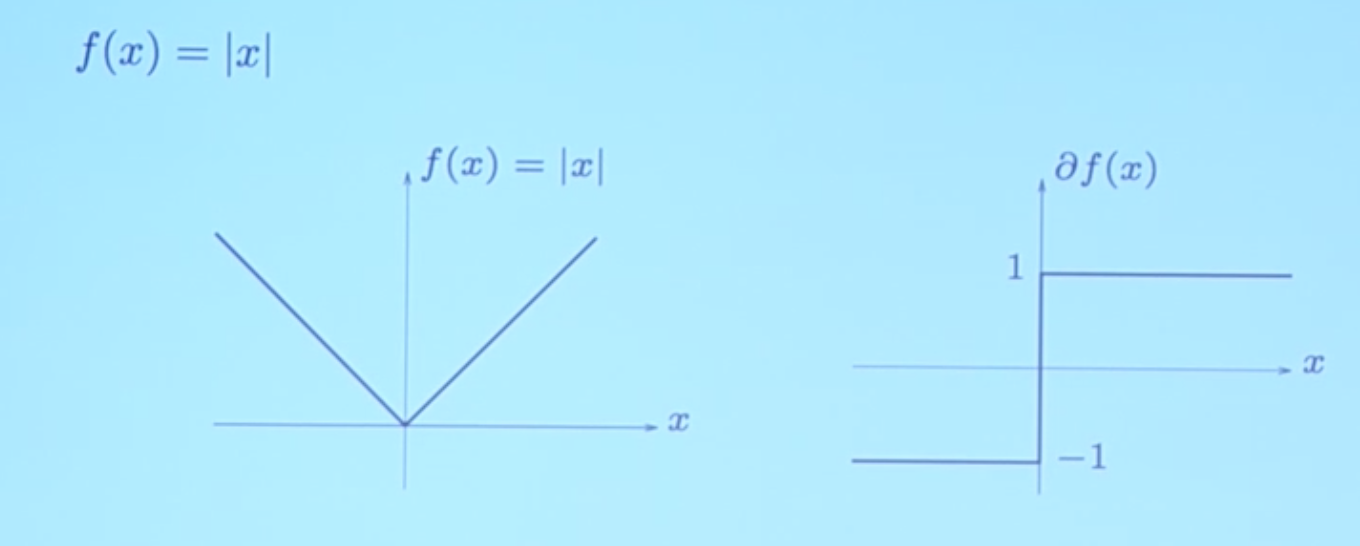
Basic Subgradient Method: Negative Subgradient Update
From [1]: Given a convex function \(f:\mathbb{R}^n \rightarrow \mathbb{R}\), not necessarily differentiable. The subgradient method is just like gradient descent, but replacing gradients with subgradients. i.e., initialize \(x^{(0)}\), then repeat
\[\begin{array}{ll} x^{(k+1)} = x^{(k)} − \alpha_k \cdot g^{(k)}, & k = 0, 1, 2, 3, \cdots \end{array}\]where \(g^{(k)}\) is any subgradient of \(f\) at \(x^{(k)}\), and \(\alpha_k >0 \) is the \(k\)’th step size.
Unlike gradient descent, in the negative subgradient update it’s entirely possible that \(-g^{(k)}\) is not a descent direction for \(f\) at \(x^{(k)}\). In such cases, we always have \(f(x^{(k+1)}) > f(x^{(k)})\), meaning an iteration of the subgradient method can increase the objective function. To resolve this issue, we keep track of best iterate \(x_{best}^k\) among \(x^{(1)}, \cdots , x^{(k)}\):
\[f(x_{best}^{(k)}) = \underset{i=1,\cdots ,k}{\mbox{ min }} f(x^{(i)})\]To update each \(x^{(i)}\), there are at least 5 common ways to select the step size, all with different convergence properties:
- Constant step size
- Constant step length
- Square summable but not summable.
- Nonsummable diminishing
- Nonsummable diminishing step lengths.
See [2] for details regarding each of these possible step size choices and the associated guarantees on convergence.
Subgradient methods for constrained problems
Primal-dual subgradient methods
Stochastic subgradient method
Mirror descent and variable metric methods
Localization methods
Localization and cutting-plane methods
Analytic center cutting-plane method
Ellipsoid method
Decomposition and distributed optimization
Primal and dual decomposition
Decomposition applications
Distributed optimization via circuits
Proximal and operator splitting methods
Proximal algorithms
Monotone operators
Monotone operator splitting methods
Alternating direction method of multipliers (ADMM)
Conjugate gradients
Conjugate-gradient method
Truncated Newton methods
Nonconvex problems
\(l_1\) methods for convex-cardinality problems
\(l_1\) methods for convex-cardinality problems, part II
Sequential convex programming
Branch-and-bound methods
References
[1] Gordon, Geoff. CMU 10-725 Optimization Fall 2012 Lecture Slides, Lecture 6.
[2] Boyd, Stephen. Subgradient Methods: Notes for EE 364B, January 2007.