Geometry of Lines and Polygons
Understanding the geometry of lines and polygons represents fundamental knowledge for graphics, computer vision, and robotics.
Table of Contents:
- Line Segment Intersection
- Polygon Winding Order
- Area of a Polygon
- Polygon Intersection Algorithms
- Computing IoU of 2 polygons
Line Segment Intersection
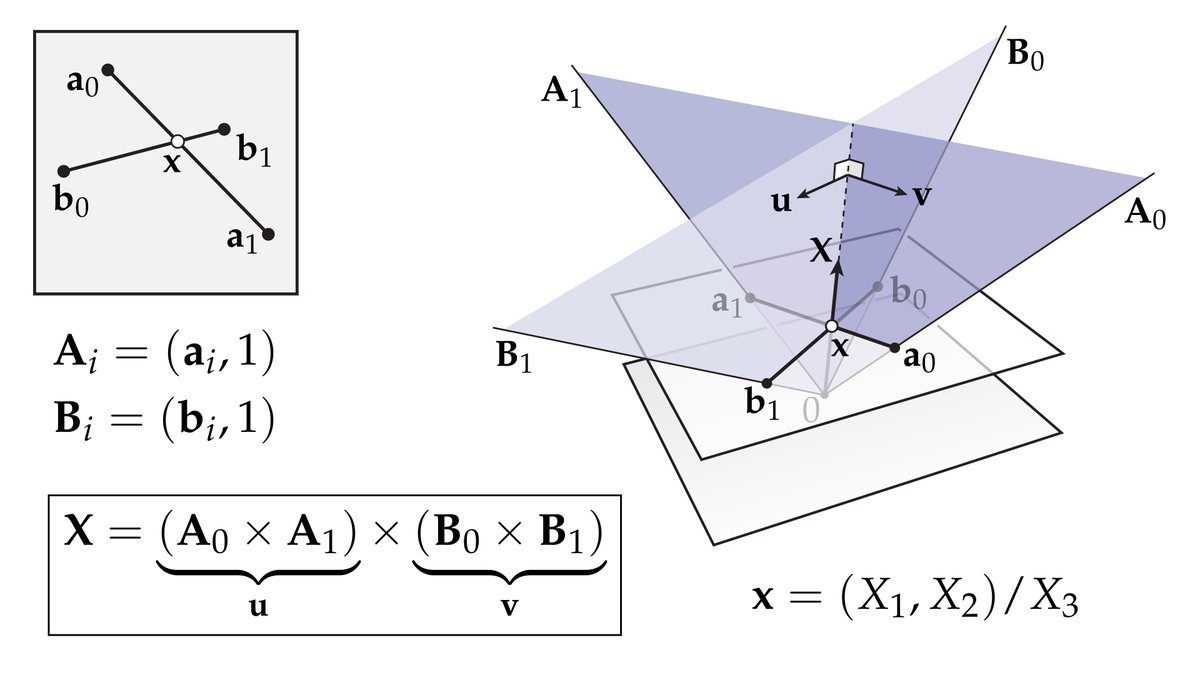
A dead-simple way to find the intersection of two line segments is by lifting them from 2d to 3d [1]:
- Append “1” to each endpoint
- Take three cross products
- Divide by the 3rd coordinate
This works because the 2D lines become 3D planes, & the cross product of the planes’ normals gives their line of intersection.
def compute_line_segment_intersection(ls_a: np.ndarray, ls_b: np.ndarray) -> Optional[np.ndarray]:
"""Compute the intersection of two line segments.
Args:
ls_a: array of shape (2,2) representing two v-stacked points
ls_b: array of shape (2,2) representing two v-stacked points
Returns:
p_i: intersection point of two line segments (possibly none if lines are parallel)
"""
a0, a1 = ls_a
b0, b1 = ls_b
def cart_to_homogeneous(p: np.ndarray) -> np.ndarray:
""" """
return np.array([p[0], p[1], 1.0])
# compute as homogeneous
u = np.cross(cart_to_homogeneous(a0), cart_to_homogeneous(a1))
v = np.cross(cart_to_homogeneous(b0), cart_to_homogeneous(b1))
x = np.cross(u, v)
if np.isclose(x[2], 0.0):
# lines are parallel, so no possible intersection!
return None
p_i = x[:2] / x[2]
return p_i
def test_compute_line_segment_intersection() -> None:
""" """
ls_a = np.array([[-4,-2],[1,3]])
ls_b = np.array([[-3,1],[-1,-1]])
p_intersect = compute_line_segment_intersection(ls_a, ls_b)
expected_p_intersect = np.array([-2., -0.])
assert np.allclose(p_intersect, expected_p_intersect)
Polygon Winding Order
def polygon_is_ccw(poly: PolygonType) -> bool:
"""Check if winding order of polygon's vertices is counter-clockwise."""
edges = get_poly_line_segments(np.array(poly))
edge_sum = 0
for i in range(len(edges)-1):
p1, p2 = edges[i]
x1, y1 = p1
x2, y2 = p2
edge_sum += (x2 - x1 ) * (y2 + y1)
return edge_sum < 0
def test_polygon_is_ccw() -> None:
"""For simple shapes, ensure that a winding order check is accurate."""
poly1 = np.array(
[
[5,0],
[6,4],
[4,5],
[1,5],
[1,0]
]
)
is_ccw = polygon_is_ccw(poly1)
assert is_ccw
# below is counter-clockwise
poly2 = np.array(
[
[2,0],
[0,2],
[-2,0],
[0,-2]
])
is_ccw = polygon_is_ccw(poly2)
assert is_ccw
# below is clockwise
poly3 = poly1[::-1]
is_ccw = polygon_is_ccw(poly3)
assert not is_ccw
Checking Location of a Point vs. Line
Another useful tool is the ability to check which side of a line segment a point is found on.
We use the determinant of two vectors (See https://stackoverflow.com/a/1560510). Line segment AB spanned by (A,B) and line segment AQ spanned by (A,Q) where Q is the query point
def point_inside_halfspace(Q: np.ndarray, ls: np.ndarray) -> bool:
"""Check which side of a line segment a point is found on.
Args:
Q: array of shape (2,) representing the query point
ls: array of shape (2,2) representing line_segment (v-stacked points). Assumes CCW order.
Returns:
whether point inside (or directly on) the halfspace defined by line segment.
"""
A, B = ls
# form 2x2 matrix.
M = np.array([B - A, Q - A])
return np.linalg.det(M) >= 0
def test_point_inside_halfspace() -> None:
""" """
p1 = np.array([0.5, 0.5])
ls = np.array([[2,0],[0,2]]) # CCW
is_inside = point_inside_halfspace(p1, ls)
assert is_inside
p1 = np.array([2,2])
is_inside = point_inside_halfspace(p1, ls)
assert not is_inside
Area of a Polygon
Shapely can compute this in a single call with shapely.geometry.Polygon(verts).area, but it’s interesting to think about how this can be implemented efficiently under the hood.
The Shoelace Formula
Compute the signed area of triangles (half of parallelogram) with determinant of 2 h-stacked vectors, and add areas.
References: https://web.archive.org/web/20100405070507/http://valis.cs.uiuc.edu/~sariel/research/CG/compgeom/msg00831.html https://en.wikipedia.org/wiki/Shoelace_formula https://www.youtube.com/watch?v=0KjG8Pg6LGk https://stackoverflow.com/a/19875560 https://stackoverflow.com/questions/451426/how-do-i-calculate-the-area-of-a-2d-polygon
def compute_polygon_area(poly: PolygonType) -> float:
"""Compute polygon area by the Shoelace formula. Polygons cannot be self-intersecting. They must be closed.
Args:
poly: input 2d polygon with N vertices.
Returns:
area of polygon.
"""
# append first vertex to the end, to close polygon.
p = np.array(poly)
p = np.vstack([p, p[0]])
x, y = p.T
# (x0 * y1) - (x1 * y0)
determinants = x[:-1] * y[1:] - x[1:] * y[:-1]
return np.absolute(np.sum(determinants)) / 2
def test_compute_polygon_area_triangle() -> None:
"""For a right triangle."""
# as CCW
poly = [
(0,0),
(2,0),
(2,2)
]
area = compute_polygon_area(poly)
assert np.isclose(area, 2.0)
def test_compute_polygon_area_square() -> None:
"""for square
"""
poly = [
(1,1),
(-1,1),
(-1,-1),
(1,-1)
]
area = compute_polygon_area(poly)
assert np.isclose(area, 4.0)
def test_compute_polygon_area_rhombus() -> None:
"""for rhombus w/ CW verts (not CCW)
"""
poly = [
(0,6),
(2,4),
(0,2),
(-2,4)
]
area = compute_polygon_area(poly)
assert np.isclose(area, 8.0)
def test_compute_polygon_area_arbitrary() -> None:
"""for arbitrary closed polygon w/ 5 verts.
"""
poly = [
(0,-2),
(2,0),
(2,2),
(0,2),
(-2,0)
]
area = compute_polygon_area(poly)
assert np.isclose(area, 10.0)
Polygon Intersection Algorithms
Shapely can compute this in a single call with Polygon(verts1).intersection(Polygon(verts2)).area
Since each polygon will be convex, can use Sutherland – Hodgman (S-H) polygon clipping (otherwise we would use Weiler–Atherton) Since both are convex polygons, can assume only 1 intersection polygon results.
References: Wikipedia
def compute_polygon_intersection(subject_polygon: PolygonType, clip_polygon: PolygonType) -> PolygonType:
"""Compute the polygon that represents the intersection of two convex polygons in a unit circle (S-H).
Args:
subject_polygon: input reference polygon with S vertices. Assumes CCW winding order.
clip_polygon: polygon to use for clipping, with C vertices. Assumes CCW winding order.
Returns:
output_polygon: list representing vertices of intersection of two input polygons.
If there is no intersection, this will be an empty list.
"""
clip_polygon = np.array(clip_polygon)
output_polygon = subject_polygon
clip_poly_segments = get_poly_line_segments(clip_polygon)
for clip_edge in clip_poly_segments:
input_polygon = np.array(output_polygon)
output_polygon = []
input_poly_segments = get_poly_line_segments(input_polygon)
for i, input_edge in enumerate(input_poly_segments):
# coming from subject.
prev_p_s, curr_p_s = input_edge
# find intersection point
p_i = compute_line_segment_intersection(ls_a=np.array([prev_p_s, curr_p_s]), ls_b=clip_edge)
# There are 3 possible cases.
if point_inside_halfspace(curr_p_s, clip_edge):
if not point_inside_halfspace(prev_p_s, clip_edge):
# entered from outside of clipping region, so we'll use the intersection point as new start point.
output_polygon.append(p_i)
output_polygon.append(curr_p_s)
# 2nd case: moving outside of the clipping region as we traverse, record intersection as new end point.
elif point_inside_halfspace(prev_p_s, clip_edge):
output_polygon.append(p_i)
# 3rd case: both points outside of clipping region, so not added to output whatsoever.
return np.array(output_polygon).tolist()
Now we’ll consider a few examples:
def test_compute_polygon_intersection_no_intersect() -> None:
"""Corresponds to Case 6: polygons do not intersect"""
poly1 = [
(-0.7071067811865476, 0.7071067811865476),
(-1, 0),
(-0.7071067811865476, -0.7071067811865476),
]
poly2 = [
(0.7071067811865476, 0.7071067811865476),
(1, 0),
(0.7071067811865476, -0.7071067811865476),
]
intersection_polygon = compute_polygon_intersection(subject_polygon=poly1, clip_polygon=poly2)
assert len(intersection_polygon) == 0
def test_compute_polygon_intersection() -> None:
"""
Two simple rectangles, with CCW vertex order.
"""
# rectangle 1
# fmt: off
rect1 = np.array(
[
[-1,-2],
[1,-2],
[1,2],
[-1,2]
])
# rectangle 2
rect2 = np.array(
[
[-2,1],
[-2,-1],
[2,-1],
[2,1]
])
# fmt: on
intersection_polygon = compute_polygon_intersection(subject_polygon=rect1, clip_polygon=rect2)
expected_intersection_polygon = [[-1.0, 1.0], [-1.0, -1.0], [1.0, -1.0], [1.0, 1.0]]
assert intersection_polygon == expected_intersection_polygon
def test_compute_polygon_intersection_2() -> None:
"""A "W" clipped to a 5-sided shape.
(see https://en.wikipedia.org/wiki/File:Sutherland-Hodgman_clipping_sample.svg)
"""
subject_polygon = np.array(
[
[47,-46],
[151,-353],
[208,-354],
[238,-254],
[266,-355],
[324,-355],
[431,-46],
[370,-45],
[297,-297],
[268,-195],
[210,-194],
[179,-294],
[105,-50]
])
clip_polygon = np.array(
[
[33,-193],
[225,-355],
[457,-192],
[254,-32],
[92,-75]
])
# draw_polygon(subject_polygon, color="g")
# draw_polygon(clip_polygon, color="r")
intersection_polygon = compute_polygon_intersection(subject_polygon, clip_polygon)
# draw_polygon(intersection_polygon, color='k')
#plt.show()
assert len(intersection_polygon) == 14
Illustrative Example: Computing IoU of 2 polygons
Given two polygons, we may wish to calculate the IoU of their areas. IoU is defined as the area of their intersection divided by the area of their union.
The vertices of the polygons are constrained to lie on the unit circle and you can assume that each polygon has at least 3 vertices, given and in sorted order.
First, instead of having to implement an algorithm to compute the union of two polygons (which is non-trivial), we can use the following insight: the union of two polygons is equal to the sum of their two areas, minus the area of their intersection.
def compute_polygon_union_area(poly1: PolygonType, poly2: PolygonType) -> PolygonType:
"""
union(1,2) = area(1) + area(2) - intersection(1,2)
"""
intersection_polygon = compute_polygon_intersection(poly1, poly2)
area_intersection = compute_polygon_area(intersection_polygon)
area_union = compute_polygon_area(poly1) + compute_polygon_area(poly2) - area_intersection
return area_union
We’ll consider a few examples to show how this works in practice:
def test_compute_polygon_union_area() -> None:
"""For simple case w/ 2 rectangles, with CCW vertex order.
"""
# rectangle 1
# fmt: off
rect1 = np.array(
[
[-1,-2],
[1,-2],
[1,2],
[-1,2]
])
# rectangle 2
rect2 = np.array(
[
[-2,1],
[-2,-1],
[2,-1],
[2,1]
])
# fmt: on
area_union = compute_polygon_union_area(poly1=rect1, poly2=rect2)
assert np.isclose(area_union, 12)
def test_compute_polygon_union_area_triangles() -> None:
""" """
# tri 1 is on top
tri1 = np.array(
[
[-2,2],
[1,-1],
[4,2]
])
# tri 2 is below
tri2 = np.array(
[
[-2,-2],
[4,-2],
[1,1]
])
area_union = compute_polygon_union_area(poly1=tri1, poly2=tri2)
assert np.isclose(area_union, 16)
Next,
import time
from typing import List, Optional, Tuple
import matplotlib.pyplot as plt
import numpy as np
import pytest
# list of 2d vertices
PolygonType = List[Tuple[float,float]]
EPSILON = 1e-10
def verify_polygon_dimension(poly: PolygonType, dim: int = 2) -> bool:
"""Check whether all vertices of a polygon satisfy desired dimensionality.
Args:
poly: input 2d polygon with N vertices.
dim: desired dimension of polygon vertices.
Returns:
whether all vertices of input polygon satisfy desired dimension.
"""
# alternatively could cast to a Numpy array, and verify it's shape
# (casted array shouldn't have "object" type if all vertices have the same dimension)
return all([len(v) == dim for v in poly])
def test_verify_polygon_dimension_valid() -> None:
"""Ensure that a 2d polygon with all 2d verts is treated appropriately."""
poly = [
(-0.1736481776669303, 0.984807753012208),
(-1, 0),
(0, -1),
]
assert verify_polygon_dimension(poly=poly, dim=2)
def test_verify_polygon_dimension_invalid() -> None:
"""Ensure we catch malformed input, e.g. a polygon with one vertex that is 3d, while the other verts are 2d."""
poly = [
(-0.1736481776669303, 0.984807753012208),
(-1, 0, 0),
(0, -1),
]
assert not verify_polygon_dimension(poly=poly, dim=2)
def verts_lie_on_unit_circle(poly: PolygonType) -> bool:
"""Check whether all vertices of a polygon lie on a unit circle.
Args:
poly: input 2d polygon with N vertices.
Returns:
whether all vertices of input polygon lie on unit circle.
"""
dists = np.linalg.norm(np.array(poly), axis=1)
return np.allclose(dists, 1.0, atol=1e-7)
def test_verts_lie_on_unit_circle_valid() -> None:
"""Verify that polygons with all vertices lying on the unit circle are treated as valid."""
poly1 = [
(-0.7071067811865475, 0.7071067811865476),
(0.30901699437494723, -0.9510565162951536),
(0.5877852522924729, -0.8090169943749476),
]
assert verts_lie_on_unit_circle(poly=poly1)
poly2 = [
(1, 0),
(0, 1),
(-1, 0),
(0, -1),
(0.7071067811865475, -0.7071067811865477),
]
assert verts_lie_on_unit_circle(poly=poly2)
def test_verts_lie_on_unit_circle_invalid() -> None:
"""Catch invalid polygon, with a single vertex lying off the unit circle."""
poly = [
(1, 0),
(0, 1),
(-1, 0),
(0,-2)
]
assert not verts_lie_on_unit_circle(poly=poly)
def convert_to_ccw(poly: PolygonType) -> PolygonType:
"""Convert a polygon with arbitrary winding order, to have CCW winding order.
https://stackoverflow.com/questions/1165647/how-to-determine-if-a-list-of-polygon-points-are-in-clockwise-order
"""
if polygon_is_ccw(poly):
# no changes necessary to get CCW
return poly
else:
# is CW, so reverse order to get CCW
return poly[::-1]
def iou(poly1: PolygonType, poly2: PolygonType) -> float:
"""Compute the intersection-over-union between two polygons.
Args:
poly1: M vertices of first 2d polygon.
poly2: N vertices of second 2d polygon.
Returns:
iou: scalar representing intersection-over-union of two polygons.
"""
poly1 = convert_to_ccw(poly1)
poly2 = convert_to_ccw(poly2)
M = len(poly1)
N = len(poly2)
# check for invalid polygons (less than 3 input verts)
if M < 3 or N < 3:
raise ValueError("Input polygons must be specified by at least 3 vertices.")
# check for invalid polygons (not an iterable of 2d vertices)
if not verify_polygon_dimension(poly1, dim=2) or not verify_polygon_dimension(poly2, dim=2):
raise ValueError("Input polygons must consist of 2-dimensional vertices.")
# check for invalid polygons (verify that all vertices lie on unit circle)
if not verts_lie_on_unit_circle(poly1) or not verts_lie_on_unit_circle(poly2):
raise ValueError("Input polygons must have all vertices on the unit circle.")
intersection_polygon = compute_polygon_intersection(poly1, poly2)
if len(intersection_polygon) == 0:
iou = 0.0 # there was no intersection
return iou
area_intersection = compute_polygon_area(intersection_polygon)
area_union = compute_polygon_area(poly1) + compute_polygon_area(poly2) - area_intersection
iou = area_intersection / (area_union + EPSILON)
return iou
def test_iou_insufficient_num_verts() -> None:
"""If one input polygon has less than 3 vertices, a ValueError should be thrown."""
poly1 = [
(1, 0),
(0, 1),
]
poly2 = [
(-0.1736481776669303, 0.984807753012208),
(-1, 0),
(0, -1),
]
with pytest.raises(ValueError):
iou(poly1, poly2)
def get_poly_line_segments(poly: np.ndarray) -> List[np.ndarray]:
"""Get line segments that define boundary of N-vertex polygon."""
N = poly.shape[0]
return [ poly[ np.array([i, (i+1) % N]) ] for i in range(N) ]
def draw_polygon(polygon: PolygonType, color: str) -> None:
"""Draw a polygon using matplotlib."""
N = len(polygon)
poly = np.array(polygon)
plt.plot(poly[:,0], poly[:, 1], color=color)
# color vertices as small circles
plt.scatter(poly[:,0], poly[:, 1], 10, marker='.', color=color)
# connect last and first vertex
plt.plot([poly[-1,0],poly[0,0]], [poly[-1,1],poly[0,1]], color=color)
# --------------------------------------------------------
def additional_test_cases() -> None:
""" """
cases = []
# Case 1: a vanilla case (see https://imgur.com/a/dSKXHPF for a diagram)
poly1 = [
(-0.7071067811865475, 0.7071067811865476),
(0.30901699437494723, -0.9510565162951536),
(0.5877852522924729, -0.8090169943749476),
]
poly2 = [
(1, 0),
(0, 1),
(-1, 0),
(0, -1),
(0.7071067811865475, -0.7071067811865477),
]
cases.append((poly1, poly2, "simple case", 0.12421351279682288))
# Case 2: another simple case
poly1 = [
(1, 0),
(0, 1),
(-0.7071067811865476, -0.7071067811865476),
]
poly2 = [
(-0.1736481776669303, 0.984807753012208),
(-1, 0),
(0, -1),
]
cases.append((poly1, poly2, "simple case 2", 0.1881047657147776))
# Case 3: yet another simple case, note the duplicated point
poly1 = [
(0, -1),
(-1, 0),
(-1, 0),
(0, 1),
]
poly2 = [
(0.7071067811865476, 0.7071067811865476),
(-0.7071067811865476, 0.7071067811865476),
(-0.7071067811865476, -0.7071067811865476),
(0.7071067811865476, -0.7071067811865476),
(0.7071067811865476, -0.7071067811865476),
]
cases.append((poly1, poly2, "simple case 3", 0.38148713966109243))
# Case 4: shared edge
poly1 = [
(-1, 0),
(-0.7071067811865476, -0.7071067811865476),
(0.7071067811865476, -0.7071067811865476),
(1, 0),
]
poly2 = [
(0, 1),
(-1, 0),
(1, 0),
]
cases.append((poly1, poly2, "shared edge", 0.0))
# Case 5: same polygon
poly1 = [
(0, -1),
(-1, 0),
(1, 0),
]
poly2 = [
(0, -1),
(-1, 0),
(1, 0),
]
cases.append((poly1, poly2, "same same", 1.0))
# Case 6: polygons do not intersect
poly1 = [
(-0.7071067811865476, 0.7071067811865476),
(-1, 0),
(-0.7071067811865476, -0.7071067811865476),
]
poly2 = [
(0.7071067811865476, 0.7071067811865476),
(1, 0),
(0.7071067811865476, -0.7071067811865476),
]
cases.append((poly1, poly2, "no intersection", 0.0))
t0 = time.time()
for poly1, poly2, description, expected in cases:
computed = iou(poly1, poly2)
print('-'*20)
print(description)
print("computed:", computed)
print("expected:", expected)
print("PASS" if abs(computed - expected) < 1e-8 else "FAIL")
assert np.isclose(computed, expected, atol=1e-8)
# details here don't matter too much, but this shouldn't be seconds
dt = (time.time() - t0) * 1000
print("done in %.4fms" % dt)
References
- Keenan Crane, “Dead-simple way to find the intersection of two line segments.” Twitter. [Link].
-
David Breen, William Regli and Maxim Peysakhov. Polygon Clipping and Filling Week 3, Lecture 5. PDF.
-
Ivan E. Sutherland , Gary W. Hodgman. Reentrant polygon clipping. Communications of the ACM, Volume 17, Issue 1. Jan. 1974. PDF.
- Sutherland Hodgman. Wikipedia