Table of Contents:

Unconstrained Optimization

The Gauss-Newton Method

Suppose our residual is no longer affine, but rather nonlinear. We want to minimize \(\lVert r(x) \rVert^2\). Generally speaking, we cannot solve this problem, but rather can use good heuristics to find local minima.

Start from initial guess for your solution
Repeat:
(1) Linearize \(r(x)\) around current guess \(x^{(k)}\). This can be accomplished by using a Taylor series and calculus (standard Gauss-Newton), or one can use a least-squares fit to the line.
(2) Solve least squares for linearized objective, get \(x^{(k+1)}\).

The linearized residual \(r(x)\) will resemble:

\[r(x) \approx r(x^{(k)}) + Dr(x^{(k)}) (x-x^{(k)})\]

where \(Dr\) is the Jacobian, meaning \( (Dr)_{ij} = \frac{\partial r_i}{\partial x_j}\)

Distributing the rightmost product, we obtain

\[\begin{aligned} r(x) & \approx r(x^{(k)}) + Dr(x^{(k)})x - Dr(x^{(k)}) (x^{(k)}) \\ r(x) & \approx Dr(x^{(k)})x - \bigg(Dr(x^{(k)}) (x^{(k)}) - r(x^{(k)}) \bigg) \end{aligned}\]

With a single variable \(x\), we can re-write the above equation as a matrix vector product \(Ax\), and a constant term \(b\):

\[r(x) \approx A^{(k)}x - b^{(k)}\]

Levenberg-Marquardt Algorithm (Trust-Region Gauss-Newton Method)

In Levenberg-Marquardt, we have add a term to the objective function to emphasize that we should not move so far from \( \theta^{(k)} \) that we cannot trust the affine approximation. We often refer to this concept as remaining within a “trust region” (TRPO (Schulman, 2015) is named after the same concept). Thus, we wish \(|| \theta - \theta^{(k)} ||^2\) to be small. Our new objective is:

\[||A^{(k)} \theta - b^{(k)}||^2 + \lambda^{(k)} || \theta − \theta^{(k)}||^2\]

This objective can be written inside a single \(\ell_2\)-norm, instead using two separate \(\ell_2\)-norms:

\[|| \begin{bmatrix} A^{(k)} \\ \sqrt{\lambda^{(k)}} I \end{bmatrix} \theta - \begin{bmatrix} b^{(k)} \\ \sqrt{\lambda^{(k)}} \theta^{(k)} \end{bmatrix} ||^2\]

See (Boyd & Vandenberghe, 2018), Section 18.3 for a more detailed description.

Binary Classification

Suppose we have some input data \(x\) and labels \(y\). Our prediction function could be

\[\hat{f} = x^T\theta_1 + \theta_2\]

Suppose at inference time we use \(f(x) = \mbox{sign }\bigg(\hat{f}(x)\bigg)\), where \(\mbox{sign }(a) = +1\) for \(a \geq 0\) and −1 for \(a < 0\). At training time, we use its smooth (and differentiable) approximation, the hyperbolic tangent, tanh:

\[\phi(u) = \frac{e^u - e^{-u}}{e^u + e^{-u}}\]

phi = lambda x: (np.exp(x)-np.exp(-x)) / (np.exp(x)+np.exp(-x))

The gradient of \(\mbox{tanh}\): \(\nabla_x \mbox{tanh } = 1-\mbox{tanh }(x)^2\). We call this \(\phi^{\prime}\) in code:

phi_prime = lambda x: 1-phi(x)**2

Suppose our objective function is the MSE loss, with a regularization term:

\[J = \sum\limits_{i=1}^{N} \Bigg(y_i - \phi\big(x_i^T\theta_1 + \theta_2\big)\Bigg)^2 + \mu ||\theta_1||^2\]

The residual for a single training example \(i\) is \(r_i\):

\[r_i = y_i - \phi\big(x_i^T\theta_1 + \theta_2\big)\]

For a vector of training examples \(\mathbf{X}\) and labels \(\mathbf{Y}\), if we name \(\theta_1,\theta_2\) as t1,t2, our nonlinear residual function is:

r = lambda x, y, t1, t2: y - phi(x @ t1 + t2)

To linearize the residual, we compute its Jacobian \(Dr(\theta_1,\theta_2)\) via matrix calculus:

\[\frac{\partial r_i}{\partial \theta_1} = -\phi^{\prime}(x_i^T\theta_1 + \theta_2)x_i^T\]

If our data was laid out with each example \(x_i\) representing a single row of \(X\), and if \(\theta = \begin{bmatrix}\theta_1 \\ \theta_2 \end{bmatrix}\) was a 401-dimension vector, with 1-d bias:

jacobian_0_entr = -phi_prime(X[i,:] @ theta[:400] + theta[-1]) * X[i,:]

\[\frac{\partial r_i}{\partial \theta_2} = -\phi^{\prime}(x_i^T\theta_1 + \theta_2)\]

jacobian_1_entr = -phi_prime(X[i,:] @ theta[:400] + theta[-1])

The the full Jacobian evaluated at a certain point \(X_i\) is just these stacked individual entries:

Dr = np.zeros((len(X), len(theta)))
for i in range(len(X)):
    jacobian_0_entr = -phi_prime(X[i,:] @ theta[:IMAGE_DIM] + theta[-1]) * X[i,:]
    jacobian_1_entr = -phi_prime(X[i,:] @ theta[:IMAGE_DIM] + theta[-1])
    Dr[i,:] = np.concatenate([jacobian_0_entr, jacobian_1_entr])

Let \(\theta= \begin{bmatrix} \theta_1^T & \theta_2 \end{bmatrix}^T \in \mathbb{R}^{401}\). The linearized residual follows the exact form outlined in the Gauss-Newton section above:

\[\begin{aligned} r(\theta) & \approx A^{(k)}\theta - b^{(k)} \\ r(\theta) & \approx Dr(\theta^{(k)})\theta - \bigg(Dr(\theta^{(k)}) (\theta^{(k)}) - r(\theta^{(k)}) \bigg) \end{aligned}\]

where

\[b^{(k)} = A^{(k)} \theta^{(k)} - r\bigg(\theta^{(k)}\bigg)\]

In code, this term is computed as:

A_k_temp = Dr # computed above
b_k_temp = Dr @ theta - r(X, Y, theta[:400], theta[-1])

We solve a least-squares problem in every iteration, with a 3-part objective function (penalizing the residual, large step sizes, and also large \(\theta_1\)-norm weights):

\[|| \begin{bmatrix} A^{(k)} \\ \sqrt{\lambda^{(k)}} I_{401} \\ \begin{bmatrix} \sqrt{\mu} I_{400 } & 0\end{bmatrix} \end{bmatrix} \theta - \begin{bmatrix} b^{(k)} \\ \sqrt{\lambda^{(k)}} \theta^{(k)} \\ 0 \end{bmatrix} ||^2.\]

We represent the left term by

A_k = np.vstack(
    [
        A_k_temp,
        np.sqrt(lambda_[itr])*np.eye(len(theta)),
        np.concat([np.sqrt(mu)*np.eye(len(theta)-1), np.zeros((len(theta)-1,1))])
    ]
)

and the right term by

b_k = np.vstack(
    [
        b_k_temp,
        np.sqrt(lambda_[itr]) * theta,
        np.zeros((len(theta)-1,1))
    ]
)

We solve for the next iterate of \(\theta\) with the pseudo-inverse. In MATLAB, this resembles theta_temp = A_k\b_k, but in Python, we’ll use the following operator, based on np.linalg.matrix_rank(A_k)

theta_temp, _, _, _ = np.linalg.lstsq(A_k, b_k)

Consider a binary classification problem for digit zero from MNIST. MNIST contains \(28 \times 28\) images. For a function \(f: \mathbb{R}^n \rightarrow \mathbb{R}^m\), then the Jacobian will be of shape \(m \times n\), e.g. for 60k examples, and a parameter vector \(\theta\) of shape (28*28)+1, the Jacobian would be \(60k \times 785\). The full algorithm might resemble:

from typing import Tuple

import matplotlib.pyplot as plt
import numpy as np
import torch
from torchvision import datasets, transforms

transform = transforms.Compose([transforms.ToTensor()])

IMAGE_DIM = 784 # 784=28*28

def _get_dataset_split(train: bool) -> Tuple[np.ndarray, np.ndarray]:
    """Obtain (X,Y) training pairs from MNIST train or validation split."""
    split_kwargs = {'batch_size': 60000 if train else 10000}
    dataset_split = datasets.MNIST(root='./mnist_data', train=train, download=train, transform=transform)
    split_loader = torch.utils.data.DataLoader(dataset_split, **split_kwargs)
    for X, Y in split_loader:
        pass

    X = X.numpy()
    X = X.reshape(-1, 28*28)
    Y = Y.numpy()
    Y = _binarize_labels(Y)

    return X, Y

def _binarize_labels(Y: np.ndarray) -> np.ndarray:
    """Modify non-digit 0 label to -1, and digit 0 label to +1."""
    is_digit0 = (Y == 0)
    Y[is_digit0] = 1
    Y[~is_digit0] = -1
    return Y

def _infer_test_set(theta: np.ndarray) -> float:
    """Perform inference with model weights `theta` on MNIST validation split."""
    X, Y = _get_dataset_split(train=False)
    Y_pred = np.sign(X @ theta[:IMAGE_DIM] + theta[-1]).astype(np.int64)
    acc = np.mean(Y_pred == Y)
    print(f"Accuracy: {acc:.3f}")
    return acc

def main() -> None:
    """ """
    X, Y = _get_dataset_split(train=True)
    
    mu = 10 # Regularization coefficient.

    # Defines initial value for theta (last entry is theta_2)
    theta = np.ones((IMAGE_DIM+1,1)) 

    # Defines lambda functions.
    phi = lambda x: (np.exp(x)-np.exp(-x)) / (np.exp(x)+np.exp(-x))
    phi_prime = lambda x: 1 - phi(x)**2

    r = lambda x, y, t1, t2: y - phi(x @ t1 + t2)

    num_iters = 15
    lambda_ = np.ones(num_iters + 1) # Initial lambda for Levenberg-Marquardt.
    per_iter_total_residual = np.full(shape=num_iters, fill_value=np.inf, dtype=np.float32)
    per_iter_accuracy = np.zeros(num_iters)

    for itr in range(num_iters):
        # Calculate Jacobian at the current iteration.
        Dr = np.zeros((len(X), len(theta)))
        for i in range(len(X)):
            jacobian_0_entr = -phi_prime(X[i,:] @ theta[:IMAGE_DIM] + theta[-1]) * X[i,:]
            jacobian_1_entr = -phi_prime(X[i,:] @ theta[:IMAGE_DIM] + theta[-1])
            Dr[i,:] = np.concatenate([jacobian_0_entr, jacobian_1_entr])

        # Linearize the objective function.
        A_k_temp = Dr # computed above
        # Note: `b_k_temp` has shape (len(X), 1)
        b_k_temp = Dr @ theta - r(X, Y.reshape(-1,1), theta[:IMAGE_DIM], theta[-1])

        A_k = np.vstack(
            [
                A_k_temp,
                np.sqrt(lambda_[itr])*np.eye(len(theta)),
                np.hstack([np.sqrt(mu)*np.eye(len(theta)-1), np.zeros((len(theta)-1,1))])
            ]
        )
        b_k = np.vstack(
            [
                b_k_temp,
                np.sqrt(lambda_[itr])*theta,
                np.zeros((len(theta)-1,1))
            ]
        )

        # Solve Ax=b.
        theta_temp, _, _, _ = np.linalg.lstsq(A_k, b_k)

        # Check if total residual decreased.
        per_iter_total_residual[itr] = np.linalg.norm(r(X, Y.reshape(-1,1), theta_temp[:IMAGE_DIM], theta_temp[-1]))

        if itr==0 or per_iter_total_residual[itr] < np.amin(per_iter_total_residual[:itr]):
            lambda_[itr+1] = lambda_[itr] * 0.8
            # Only if total residual decreased, update weights.
            theta = theta_temp
        else:
            lambda_[itr+1] = lambda_[itr] * 2

        per_iter_accuracy[itr] = _infer_test_set(theta)
        # Define stopping condition ...

    fig, axes = plt.subplots(1, 3)
    fig.suptitle('LM for MNIST Results')
    axes[0].set_title("Total residual \nvs. iteration #")
    axes[0].scatter(range(num_iters),per_iter_total_residual, 10, color='g', marker='.')
    axes[0].plot(range(num_iters),per_iter_total_residual, color='g')
    axes[0].set_xlabel("Iteration #")
    axes[0].set_ylabel("Total residual")

    axes[1].set_title("Classification accuracy \nvs. iteration #")
    axes[1].scatter(range(num_iters), per_iter_accuracy, 10, color='b', marker='.')
    axes[1].plot(range(num_iters), per_iter_accuracy, color='b')
    axes[1].set_xlabel("Iteration #")
    axes[1].set_ylabel("Accuracy")

    axes[2].set_title(r"$\lambda$")
    axes[2].scatter(range(num_iters), lambda_[:-1], 10, color='r', marker='.')
    axes[2].plot(range(num_iters), lambda_[:-1], color='r')
    axes[2].set_xlabel("Iteration #")
    axes[2].set_ylabel(r"$\lambda$")
    plt.show()

if __name__ == '__main__':
    main()

Results: Toy Example for MNIST

Below, we’ll show the results from running LM on our MNIST dataset above:

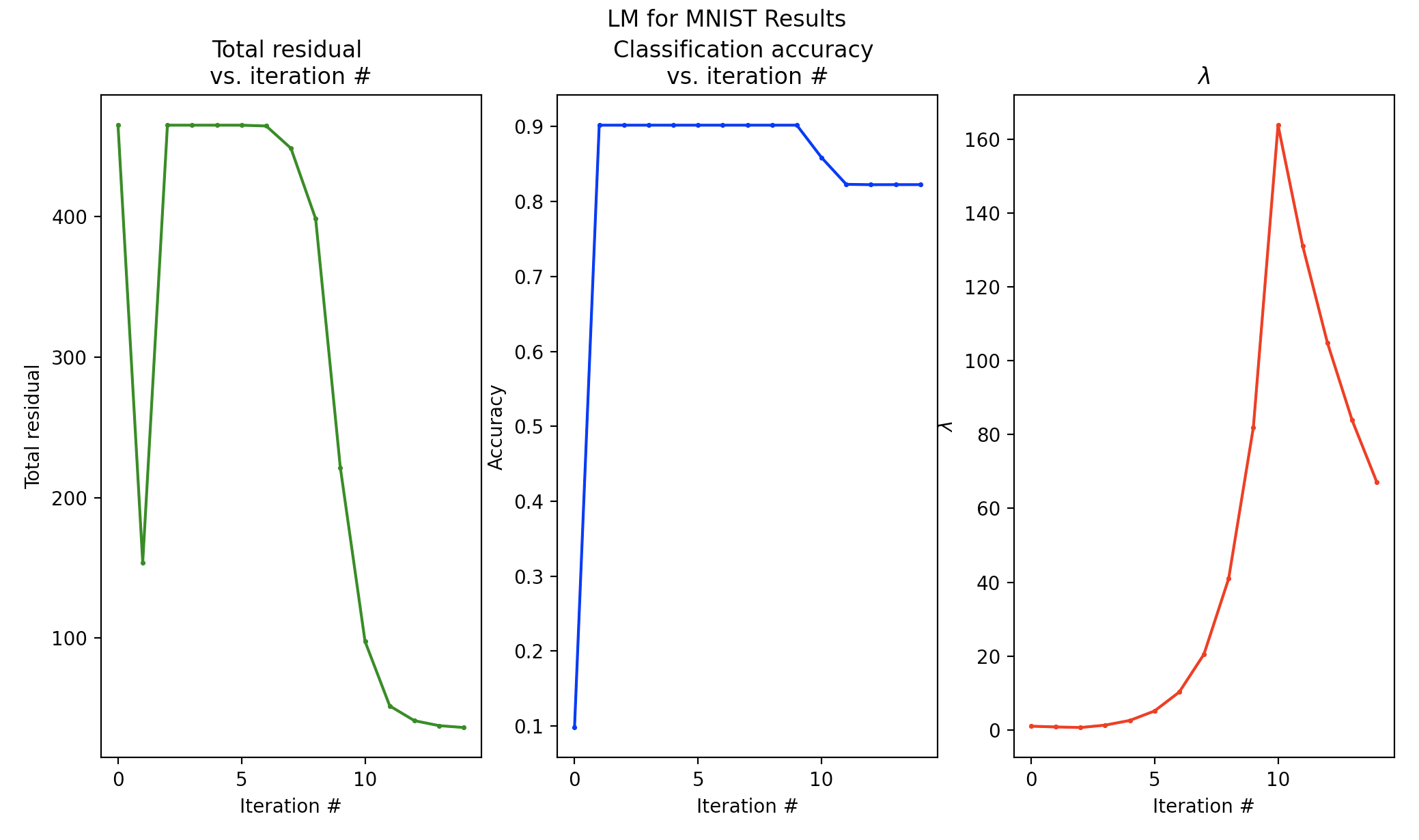
We achieved over 80% accuracy in classifying digit-0 images, and we used no deep learning.

Performant Implementations: GTSAM

Running the code above should take about 1-2 minutes on your machine. For a more performant implementation, see GTSAM’s LM class (implemented in C++). We show selected portions of the implementation below:

bool LevenbergMarquardtOptimizer::tryLambda(const GaussianFactorGraph& linear,
                                            const VectorValues& sqrtHessianDiagonal) {
  ...
  // Build damped system for this lambda (adds prior factors that make it like gradient descent)
  auto dampedSystem = buildDampedSystem(linear, sqrtHessianDiagonal);
  
  double newError = numeric_limits<double>::infinity(), costChange;
  Values newValues;
  VectorValues delta;
  delta = solve(dampedSystem, params_);
  
  double oldLinearizedError = linear.error(VectorValues::Zero(delta));
  double newlinearizedError = linear.error(delta);
  
  // cost change in the linearized system (old - new)
  double linearizedCostChange = oldLinearizedError - newlinearizedError;
  if (linearizedCostChange >= 0) {  // step is valid

    // ============ This is where the solution is updated ====================
    newValues = currentState->values.retract(delta);

    newError = graph_.error(newValues);

    // cost change in the original, nonlinear system (old - new)
    costChange = currentState->error - newError;

    if (linearizedCostChange > std::numeric_limits<double>::epsilon() * oldLinearizedError) {
      // the (linear) error has to decrease to satisfy this condition
      // fidelity of linearized model VS original system between
      modelFidelity = costChange / linearizedCostChange;
      // if we decrease the error in the nonlinear system and modelFidelity is above threshold
      step_is_successful = modelFidelity > params_.minModelFidelity;
    }
    if (step_is_successful) {
      // we have successfully decreased the cost and we have good modelFidelity
      state_ = currentState->decreaseLambda(params_, modelFidelity, std::move(newValues), newError);
    }
	...
}

References

[1] John Schulman, Sergey Levine, Philipp Moritz, Michael I. Jordan, Pieter Abbeel. Trust Region Policy Optimization. [PDF].

[2] Stephen Boyd. Introduction to Applied Linear Algebra: Vectors, Matrices, and Least Squares (VMLS). Section 18.2 (Pages 387-394) [PDF].

[3] K. Madsen, H.B. Nielsen, O. Tingleff. Methods for Non-Linear Least Squares Problems. 2nd Edition, April 2004. [PDF].

[4]. Kenneth Levenberg. A Method for the Solution of Certain Non-Linear Problems in Least Squares”. Quarterly of Applied Mathematics. 1944.

[5] Donald Marquardt. An Algorithm for Least-Squares Estimation of Nonlinear Parameters. 1963. SIAM Journal on Applied Mathematics.