Table of Contents:

What is State Estimation?

State estimation is the study of reproducing the state of a robot (e.g. its orientation, location) from noisy measurements. Unfortunately, we can’t obtain the state \(x\) directly. Instead, we can obtain get a measurement that is all tangled up with noise.

A more formal definition: Given a history of measurements \((y_1, \dots, y_t)\), and system inputs \((u_1, \dots, u_t)\), find an estimate \(\hat{x}_t\) of the state \(x\) with small error \(\|\hat{x}_t - x_t \|\).

What do we have to work with?

  • (1) We are given the measurements \(y_t\), whose distribution is modeled as \(p(y_t \mid x_t, u_t)\).
  • (2) We assume that we know the state transition distribution \(p(x_{t+1} \mid x_t, u_t)\), i.e. the robot dynamics.

The goal of state estimation is to find the posterior distribution of \(x\) given all of the prior measurements and inputs:

\[p(x_t \mid y_{1:t}, u_{1:t})\]

Why do we need a distribution instead of a single state estimate?

The goal of state estimation is not to obtain a single \(\hat{x}\). Rather, we desire a distribution over \(x\)’s. You might ask, why?

The mean of a distribution may not be representative of the distribution whatsoever. For example, consider a bimodal distribution with a mean around 0, but consisting of two camel humps. There is more information in the Bayesian estimate that we can use for control. In the case of a Kalman Filter, we will express the state distribution as a Gaussian, which is parameterized compactly by a mean and covariance.

Discrete-time Linear Dynamical Systems (DT LDS)

Filtering and estimation is much more easily described in discrete time than in continuous time. We use Linear Dynamical Systems as a key tool in state estimation.

Suppose we have a system with state \(x \in R^n\), which changes over timesteps \(t\) [1,2]. The matrix \(A(t) \in R^{n \times n}\) is called the dynamics matrix. Suppose we provide an input \(u \in R^m\) at time \(t\). \(B(t)\) is the \(R^{n \times m}\) input matrix. The vector \(c(t) \in R^n\) is called the offset. We can express the system as:

\[x(t + 1) = A(t)x(t) + B(t)u(t) + c(t)\]

We will use the shorthand notation for simplicity:

\[x_{t + 1} = A_t x_t + B_t u_t + c_t\]

As Boyd and Vandenberghe point out [2], the LDS is a “special case of a Markov system where the next state is a linear function of the current state.” Suppose we also have an output of the system \(y(t) \in R^{p}\). \(C(t) \in R^{p \times n}\) is the output or sensor matrix. This equation can be modeled as:

\[y(t) = C(t)x(t) + D(t)u(t)\]

or in shorthand, as

\[y_t = C_t x_t + D_t u_t\]

where \(t \in Z = \{0, \pm 1, \pm 2, \dots \}\) and vector signals \(x,u,y\) are sequences. It is not hard to see that the DT LDS is a first-order vector recursion [1].

Probability Review: The Chain Rule, Marginalization, & Bayes Rule

The Chain Rule states that if \(y_1,...y_t\) are events, and \(p(y_i) > 0\), then:

\[p(y_1 \cap y_2 \cap \dots \cap y_t) = p(y_1) p(y_2 \mid y_1)···p(y_t \mid y_1 \cap \dots \cap y_{t-1})\]

Marginalization is a method of variable elimination. If \(X_1,X_2\) are independent:

\[\int\limits_{x_2} p(x_1,x_2) dx_2 = \int\limits_{x_2} p(x_1)p(x_2)dx = p(x_1) \int\limits_{x_2} p(x_2)dx_2 = p(x_1)\]

We recall Bayes’ Rule states that if \(x,y\) are events, and \(p(x) > 0\) and \(p(y) > 0\), then:

\[p(x \mid y) = \frac{p(y \mid x)p(x)}{p(y)} = \frac{p(y,x)}{p(y)}\]

In the domain of state estimation, we can assign the following meaning to these distributions:

  • \(p(x)\) is our prior.
  • \(p(y \mid x)\) is our measurement likelihood.
  • \(p(y)\) is the normalization term.
  • \(p(x \mid y)\) is our posterior (what we can’t see, given what we can see).

One problem is that we may not know \(p(y)\) directly. Fortunately, it turns out we don’t need to. By marginalization of \(x\) from the joint distribution \(p(x,y)\), we can write the normalization constant \(p(y)\) in the denominator differently:

\[p(x \mid y) = \frac{p(y \mid x) p(x)}{\int\limits_x p(y\mid x)p(x) dx}\]

Recursive Bayesian Estimation + Conditional Independence

In estimation, the state \(X\) is static. In filtering, the state \(X\) is dynamic. We will address the Bayesian estimation case first, which can be modeled graphically as Naive Bayes, and later we’ll address the Bayesian filtering case.

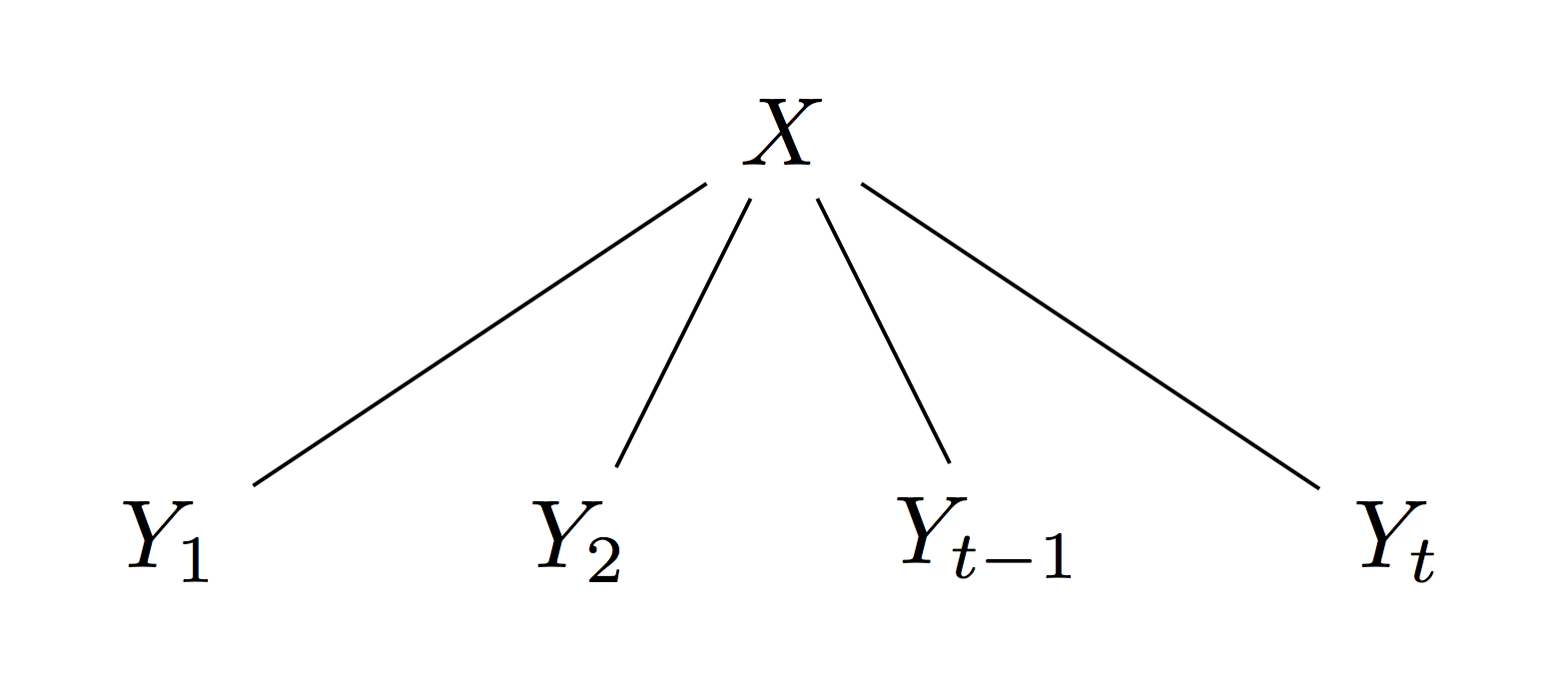
Suppose we have sequence of measurements (Y_1,Y_2,..., Y_t), revealed. X is a static state. Assume Y_1,..., Y_t are conditionally independent given X. This is the Naive Bayes' structure of Bayesian estimation.

Bayes Estimator Derivation

We’ll now derive the estimator’s recursion, which iterates upon the previous timesteps. The key insight is that we can factor Bayes Rule via conditional independence.

Suppose we have observed a measurement \(y\) for \(t-1\) timesteps. In the previous time step we had posterior:

\[p(x \mid y_{1:t-1}) = \frac{p(y_{1:t-1} \mid x) p(x)}{\int\limits_x p(y_{1:t-1}\mid x)p(x) dx}\]

We want to compute: \(p(x \mid y_{1:t}) = \frac{p(y_{1:t} \mid x) p(x)}{\int\limits_x p(y_{1:t}\mid x)p(x) dx}\)

By the Chain Rule: \(p(x \mid y_{1:t}) = \frac{ p(y_t, x, y_{1:t-1}) }{\int\limits_x p(y_{1:t}, x) dx} = \frac{ p(y_t \mid x, y_{1:t-1}) p(y_{1:t-1} \mid x) p(x)}{\int\limits_x p(y_{1:t}\mid x)p(x) dx}\)

We assume that conditioned upon \(x\), all \(y_i\) are conditionally independent. Thus, we can discard evidence: \(p(y_t \mid x, y_{1:t-1}) = p(y_t \mid x)\). Simplifying, we see:

\[p(x \mid y_{1:t}) = \frac{ p(y_t \mid x) p(y_{1:t-1} \mid x) p(x)}{\int\limits_x p(y_t \mid x) p(y_{1:t-1} \mid x) p(x) dx}\]

At this point, we may divide the numerator and denominator by any quantity of our choice, without changing the value of the expression. Suppose we choose (conveniently, as we’ll see) to divide both by \(\int\limits_x p(y_{1:t-1}\mid x)p(x) dx\):

\[p(x \mid y_{1:t}) = \frac{ p(y_t \mid x) p(y_{1:t-1} \mid x) p(x)}{\int\limits_x p(y_t \mid x) p(y_{1:t-1} \mid x) p(x) dx} = \frac{ p(y_t \mid x) \frac{p(y_{1:t-1} \mid x) p(x)}{\int\limits_x p(y_{1:t-1}\mid x)p(x) dx} }{ \frac{\int\limits_x p(y_t \mid x) p(y_{1:t-1} \mid x) p(x) dx}{\int\limits_x p(y_{1:t-1}\mid x)p(x) dx} }\]

Now we will do a bit of simplification, which will allow us to rewrite this expression in terms of the posterior from the previous time step, i.e. \(p(x \mid y_{1:t-1})\). We see the previous time step’s posterior also included \(p(y_{1:t-1} \mid x) p(x)\) (the unnormalized previous time step posterior). We can simplify as follows:

\[p(x \mid y_{1:t}) = \frac{ p(y_t \mid x) p(x \mid y_{1:t-1}) }{ \frac{\int\limits_x p(y_t \mid x) p(y_{1:t-1} \mid x) p(x) dx}{\int\limits_x p(y_{1:t-1}\mid x)p(x) dx} }\]

We can now combine these integrals into a single integral (since constant w.r.t. integral):

\[p(x \mid y_{1:t}) = \frac{ p(y_t \mid x) p(x \mid y_{1:t-1}) }{ \int\limits_x \frac{ p(y_t \mid x) p(y_{1:t-1} \mid x) p(x) }{ \int\limits_x p(y_{1:t-1}\mid x)p(x) dx} dx} = \frac{ p(y_t \mid x) p(x \mid y_{1:t-1}) }{ \int\limits_x p(y_t \mid x) \frac{ p(y_{1:t-1} \mid x) p(x) }{\int\limits_x p(y_{1:t-1}\mid x)p(x) dx} dx}\]

When grouped differently, as shown on the far right, we see the previous posterior lurking in its unsimplified form in the denominator. We can use its simplified form to show:

\[p(x \mid y_{1:t}) = \frac{p(y_t \mid x) p(x \mid y_{1:t-1})}{ \int\limits_x p(y_t \mid x) p(x \mid y_{1:t-1})dx} = f\Bigg(y_t, p(x \mid y_{1:t-1}) \Bigg)\]

In the recursive Bayes Estimator, the prior is just the posterior from the previous time step. Thus, we have the following loop: Measure->Estimate->Measure->Estimate…. We only got this from conditional independence of measurements, given the state. The graphical model is Naive Bayes.

Graphical Model: The Structure of Variables in the Bayes Filter

Now consider a dynamic state \(X_t\), instead of a static \(X\). This system can be modeled as a Hidden Markov Model. The model is hidden because we can’t see the \(X\)’s correctly. Given only the measurements, we try to back out/predict what the state was.

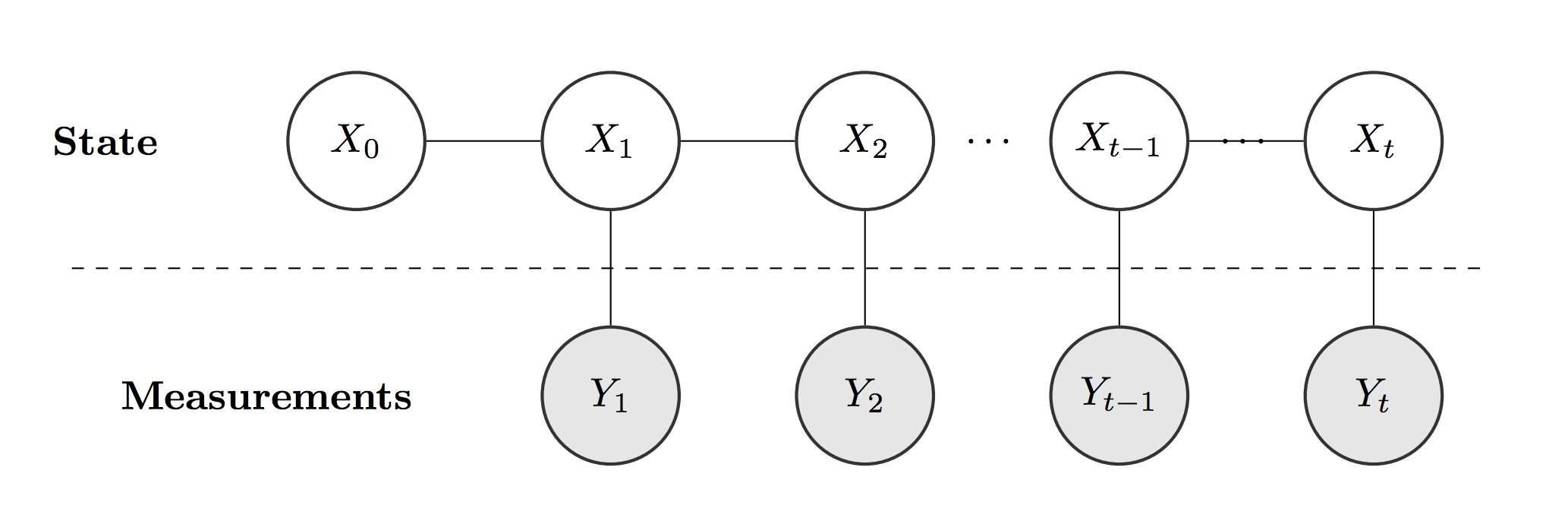
As we move forward in time, the state evolves from $$X_0 \rightarrow X_1 \rightarrow \dots \rightarrow X_t$$

The HMM structure gives us two gifts: (1) the Markov Property, and (2) Conditional Independence.

The Markov Property (Markovianity): discard information regarding the state

\[p(x_t \mid x_{1:t-1}, y_{1:t-1}) = p(x_t \mid x_{t-1})\]

Conditional Independence of Measurements: discard information regarding the measurement

\[p(y_t \mid x_{1:t}, y_{1:t-1}) = p(y_t \mid x_t)\]

What is the intution behind this last assumption? The measurement at any time step, given the state at that time step, is independent of everything else! Since the measurement is current, knowing the past (now inaccurate measurements) wouldn’t help.

Derivation of the Bayes Filter: Predict Step

In the predict step, we will make an estimate about the current value of our state, given only the prior measurements. Suppose we start with our posterior from the previous timestep, which incorporates all measurements \(y_1,\dots, y_{t-1}\). Via marginalization, we can rewrite the expression as:

\[p(x_{t} \mid y_{1:t-1}) = \int_{x_{t-1}} p(x_{t}, x_{t-1} \mid y_{1:t-1})dx_{t-1}\]

By the chain rule, we can factor:

\[p(x_{t} \mid y_{1:t-1}) = \int_{x_{t-1}} p(x_{t}, \mid x_{t-1}, y_{1:t-1}) p( x_{t-1} \mid y_{1:t-1}) dx_{t-1}\]

By Markovianity, we can simplify the expression above, giving us the Predict Step:

\[p(x_{t} \mid y_{1:t-1}) = \int_{x_t-1} p(x_{t} \mid x_{t-1}) p(x_{t-1} \mid y_{1:t-1})dx_{t-1}\]

Derivation of the Bayes Filter: Update Step

In what we call the update step, we use the current measurement to estimate the current state. We simply express the posterior using Bayes’ Rule. Once again, we compute the denominator only by marginalization:

\[p(x_{t} \mid y_{1:t}) = \frac{p(y_{1:t} \mid x_{t}) p(x_{t})}{p(y_{1:t})} = \frac{p(y_{1:t} \mid x_{t}) p(x_{t})}{\int\limits_{x_{t}} p(y_{1:t} \mid x_{t}) p(x_{t}) dx_{t}}\]

We can now factor the numerator with the chain rule:

\[p(x_{t} \mid y_{1:t}) = \frac{ p(y_t \mid x_t, y_{1:t-1}) p(y_{1:t-1} \mid x_{t}) p(x_{t})}{\int\limits_{x_{t}} p(y_t \mid x_t, y_{1:t-1}) p(y_{1:t-1} \mid x_{t}) p(x_{t})dx_{t}}\]

By the conditional independence of measurements \(y\), we know \(p(y_t \mid x_t, y_{1:t-1}) = p(y_t \mid x_t)\), so we can simplify:

\[p(x_{t} \mid y_{1:t}) = \frac{ p(y_t \mid x_t) p(y_{1:t-1} \mid x_{t}) p(x_{t})}{\int\limits_{x_{t}} p(y_t \mid x_t) p(y_{1:t-1} \mid x_{t}) p(x_{t})dx_{t}}\]

Interestingly enough, we can see above in the right hand side two terms from Bayes’ Rule. We’ll be able to collapse them into a single term. Using these two terms, the left side of Bayes’ Rule would be:

\[p(x_t \mid y_{1:t-1}) = \frac{p(y_{1:t-1} \mid x_{t}) p(x_{t})}{ \int_{x_t}p(y_{1:t-1} \mid x_{t}) p(x_{t}) dx_t }\]

Multiplying by the denominator, we obtain:

\[p(x_t \mid y_{1:t-1}) \int_{x_t}p(y_{1:t-1} \mid x_{t}) p(x_{t}) dx_t = p(y_{1:t-1} \mid x_{t}) p(x_{t})\]

Since by marginalization \(\int_{x_t}p(y_{1:t-1} \mid x_{t}) p(x_{t}) dx_t = p(y_{1:t-1})\), we can simplify the line above to:

\[p(x_t \mid y_{1:t-1}) p(y_{1:t-1}) = p(y_{1:t-1} \mid x_{t}) p(x_{t})\]

We now plug this substitution into the numerator and in the denominator of the posterior:

\[p(x_{t} \mid y_{1:t}) = \frac{ p(y_t \mid x_t) p(x_t \mid y_{1:t-1}) p(y_{1:t-1}) }{\int\limits_{x_{t}} p(y_t \mid x_t) p(x_t \mid y_{1:t-1}) p(y_{1:t-1}) dx_{t}}\]

Since \(p(y_{1:t-1})\) does not depend upon \(x\), we can pull it out of the integral, and the term cancels in the top and bottom:

\[p(x_{t} \mid y_{1:t}) = \frac{ p(y_t \mid x_t) p(x_t \mid y_{1:t-1}) p(y_{1:t-1}) }{ p(y_{1:t-1})\int\limits_{x_{t}} p(y_t \mid x_t) p(x_t \mid y_{1:t-1}) dx_{t}} = \frac{ p(y_t \mid x_t) p(x_t \mid y_{1:t-1}) }{ \int\limits_{x_{t}} p(y_t \mid x_t) p(x_t \mid y_{1:t-1}) dx_{t}}\]

This is the closed form expression for the Update Step of the Bayes’ Filter. Note that we use the result of our prediction to make the update:

\[p(x_{t} \mid y_{1:t}) = \frac{p(y_{t} \mid x_{t})p(x_{t} \mid y_{1:t-1})}{\int\limits_{x_{t}} p(y_{t} \mid x_{t}) p(x_{t} \mid y_{1:t-1}) dx_{t}}\]

The algorithm consists of repeatedly applying two steps: (1) the predict step, where we move forward the time step, and (2) the update step, where we incorporate the measurement. They appear in an arbitrary order and constitute a cycle, but you have to start somewhere. At the end of the update step, we have the best estimate.

It turns out that we can write out these integrals analytically for a very special family of distributions: Gaussian distributed random variables. This will be the Kalman Filter, which is covered in the next blog post in the State Estimation module.

References

[1] Stephen Boyd and Reza Mahalati. Lecture 1, Introduction to Linear Dynamical Systems (EE 263). http://ee263.stanford.edu/lectures/overview.pdf.

[2] Stephen Boyd and Lieven Vandenberghe. Introduction to Applied Linear Algebra – Vectors, Matrices, and Least Squares. Cambridge University Press, 2018. https://web.stanford.edu/~boyd/vmls/vmls.pdf

[3] Mac Schwager. Lecture Presentations of AA 273: State Estimation and Filtering for Aerospace Systems, taught at Stanford University in April-June 2018.